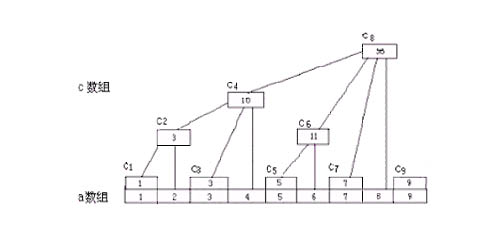
问题描述
已知数组 a 以及若干个查询 $(x, y)$,求 $a[x..y]$ 之间的最小值。
分析
不难发现:若取 t 使得$2^t\leq y-x+1$且$2^{t+1}>y-x+1$,则有:
$$[x, x+t]\bigcup[y-t+1,y]=[x,y]$$
运用二进制的思想,我们只需预处理出 $i..i+2^k-1$ 之间的最小值,即可快速完成查询。设 $dp[i][j]$ 为 $i..i+2^j-1$ 之间的最小值,则有:
$$dp[i][j]=min(dp[i][j-1],dp[i+2^{j-1}][j-1])$$
Code
var
a: array [1..100000] of longint;
dp: array [1..100000, 0..20] of longint;
n, i: longint;
function min(x, y: longint): longint;
begin
if x < y then exit(x) else exit(y);
end;
procedure init;
var
i, j: longint;
begin
for i := 1 to n do dp[i, 0] := a[i];
j := 1;
while 1<<j-1<=n do
begin
for i := 1 to n-1<<(j-1) do
dp[i, j] := min(dp[i, j-1], dp[i+1<<(j-1), j-1]);
inc(j);
end;
end;
function query(x, y: longint): longint;
var
t: longint;
begin
t := 0;
while (1<<(t+1)<=y-x+1) do inc(t);
query := min(dp[x][t], dp[y-(1<<t)+1][t]);
end;
var
x, y: longint;
begin
assign(input, 'main.in'); reset(input);
assign(output, 'main.out'); rewrite(output);
readln(n);
for i := 1 to n do read(a[i]);
init;
while not eof do
begin
read(x, y);
writeln(query(X, y));
end;
close(input); close(output);
end.