在 Ubuntu 下更改 MYSQL 的字符集

2014-11-28 | Memo

修改 /etc/mysql/my.cnf：

[client]
default-character-set=utf8

[mysqld]
character_set_server=utf8

[mysql]
default-character-set=utf8

然后 sudo service mysql restart

LCA 之离线 Tarjan 算法

2014-11-02 | Tech

真是巧妙的算法！

比起树上倍增，Tarjan 算法实现起来更为简单，一个 DFS 加并查集即可。缺点便是：需要先把所有的查询都读进来，并且要储存结果。复杂度为 $O(n+q)$。

Code

var
    sets: array [1..100] of longint;
    visited: array [1..100] of Boolean;
    a: array [1..100, 1..100] of Boolean;
    questions: array [1..1000] of record
        x, y: longint;
        ans: longint;
    end;
    qn, n, i, m, x, y, root: longint;

function find(x: longint): longint;
begin
    if x = sets[x] then exit(x);
    sets[x] := find(sets[x]);
    exit(sets[x]);
end;

procedure dfs(x: longint);
var
    i: longint;
begin
    visited[x] := true;
    //对于两个节点都已访问到的询问，其结果已经出来了
    for i := 1 to qn do
    begin
        if visited[questions[i].x] and visited[questions[i].y] then
            if questions[i].x = x then
                questions[i].ans := find(questions[i].y)
            else if questions[i].y = x then
                questions[i].ans := find(questions[i].x);
    end;
    for i := 1 to n do
    begin
        if not a[i, x] or visited[i] then continue;
        dfs(i);
        sets[find(i)] := x;
    end;
end;

begin
    assign(input, 'main.in'); reset(input);
    assign(output, 'main.out'); rewrite(output);

    read(n, m);
    for i := 1 to n do
        sets[i] := i;
    for i := 1 to m do
    begin
        read(x, y);
        a[x, y] := true;
        a[y, x] := True;
    end;
    read(root);
    qn := 0;
    while not eof do
    begin
        inc(qn);
        read(questions[qn].x, questions[qn].y);
    end;
    dfs(root);
    for i := 1 to qn do
        writeln(questions[i].ans);

    close(input); close(output);
end.

LCA 树上倍增

2014-11-02 | Tech

var
    a: array [1..100, 1..100] of boolean;
    depth: array [1..100] of longint;
    father: array [1..100, 0..16] of longint;
    n, m, i, x, y: longint;
    root: longint;

procedure dfs(x: longint);
var
    i: longint;
    j: longint;
begin
    depth[x] := depth[father[x][0]]+1;
    j := 1;
    while 1<<j<=depth[x]-1 do
    begin
        father[x][j] := father[father[x][j-1]][j-1];
        inc(j);
    end;
    for i := 1 to n do
    begin
        if not a[x][i] or (father[x][0] = i) then continue;
        father[i][0] := x;
        dfs(i);
    end;
end;

procedure swap(var x, y: longint);
var
    t: longint;
begin
    t := x;
    x := y;
    y := t;
end;

function lca(x, y: longint): longint;
var
    t, j: longint;
begin
    if depth[x] < depth[y] then
        swap(x, y);

    t := depth[x] - depth[y];
    for j := 0 to 15 do
        if t and (1<<j) <> 0 then
            x := father[x][j];
    if x = y then
        exit(x);
    for j := 15 downto 0 do
        if father[x][j] <> father[y][j] then
        begin
            x := father[x][j];
            y := father[y][j];
        end;
    lca := father[x][0];
end;

begin
    assign(input, 'main.in'); reset(input);
    assign(output, 'main.out'); rewrite(output);

    read(n, m);
    for i := 1 to m do
    begin
        read(x, y);
        a[x, y] := true;
        a[y, x] := true;
    end;
    read(root);
    father[root][0] := root;
    dfs(root);
    while not eof do
    begin
        read(x, y);
        writeln(lca(x, y));
    end;

    close(input); close(output);
end.

RMQ（二进制方法）

2014-11-02 | Tech

问题描述

已知数组 a 以及若干个查询 $(x, y)$，求 $a[x..y]$ 之间的最小值。

分析

不难发现：若取 t 使得$2^t\leq y-x+1$且$2^{t+1}>y-x+1$，则有：

$$[x, x+t]\bigcup[y-t+1,y]=[x,y]$$

运用二进制的思想，我们只需预处理出 $i..i+2^k-1$ 之间的最小值，即可快速完成查询。设 $dp[i][j]$ 为 $i..i+2^j-1$ 之间的最小值，则有：

$$dp[i][j]=min(dp[i][j-1],dp[i+2^{j-1}][j-1])$$

Code

var
    a: array [1..100000] of longint;
    dp: array [1..100000, 0..20] of longint;
    n, i: longint;

function min(x, y: longint): longint;
begin
    if x < y then exit(x) else exit(y);
end;

procedure init;
var
    i, j: longint;
begin
    for i := 1 to n do dp[i, 0] := a[i];
    j := 1;
    while 1<<j-1<=n do
    begin
        for i := 1 to n-1<<(j-1) do
            dp[i, j] := min(dp[i, j-1], dp[i+1<<(j-1), j-1]);
        inc(j);
    end;
end;

function query(x, y: longint): longint;
var
    t: longint;
begin
    t := 0;
    while (1<<(t+1)<=y-x+1) do inc(t);
    query := min(dp[x][t], dp[y-(1<<t)+1][t]);
end;

var
    x, y: longint;

begin
    assign(input, 'main.in'); reset(input);
    assign(output, 'main.out'); rewrite(output);

    readln(n);
    for i := 1 to n do read(a[i]);
    init;
    while not eof do
    begin
        read(x, y);
        writeln(query(X, y));
    end;

    close(input); close(output);
end.

树状数组

2014-11-01 | Tech

介绍

所谓树状数组，就是将线性的数组预处理成树状的结构以降低时间复杂度。先来看一幅经典的图：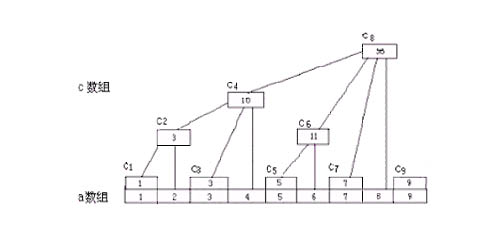

其中的 a 数组为原生数组，c 数组为辅助数组，计算方式为：

$$c_1=a_1——{(1)}_{10}={(1)}_2$$ $$c_2=a_2+c_1——{(2)}_{10}={(10)}_2$$ $$\ldots$$

不难发现，$c_k$存储的实际上是从 $k$ 开始向前数 $k$ 的二进制表示中右边第一个 $1$ 所代表的数字个元素的和。这样写的好处便是可以利用位运算轻松计算 sum。上代码。

Code

var
    n, i: longint;
    a, c: array [1..10000] of longint;

//计算x最右边的1所代表的数字。
//如：lowbit(0b1100)=0b100
function lowbit(x: longint): longint;
begin
    lowbit := x and (-x);
end;

//给a[index]加上x
procedure add(index, x: longint);
begin
    inc(a[index], x);
    while index<=n do
    begin
        inc(c[index], x);
        inc(index, lowbit(index));
    end;
end;

//求a[1~index]的和
function sum(index: longint): longint;
begin
    sum := 0;
    while index>0 do
    begin
        inc(sum, c[index]);
        dec(index, lowbit(index));
    end;
end;

var
    s: longint;
    op: longint;
    x,y: longint;

begin
    assign(input, 'main.in'); reset(input);
    assign(output, 'main.out'); rewrite(output);

    readln(n);
    for i := 1 to n do
    begin
        read(a[i]);
        add(i, a[i]);
    end;

    while not eof do
    begin
        read(op);
        if op = 1 then //添加操作
        begin
           read(x, y);
           Add(x, y);
        end
        else           //求和操作
        begin
            read(s);
            writeln(sum(s));
        end;
    end;

    close(input); close(output);
end.

二进制的启示

2014-11-01 | Tech

在学习数论时我们都知道：只用 2 的幂次可以组合出所有的正整数。这便是二进制的魅力——状态简单而又变化万千。

引子

实际算法中，常常有一些线性的但数据量特别大的问题，如区间求和、求最小值等。很多时候，为了把时间复杂度从 $O(n^2)$ 甚至更高的地方降下来，我们需要对数据进行一些预处理，以提高计算的速度。在这其中，有很大一部分是来自二进制运算特点的启发。

最小生成树（Kruscal & Prim）

2014-10-26 | Tech

测试位置：WikiOI1078

type
    TEdge = record
        start, terminal: longint;
        weight: int64;
    end;
    TEdgeArr = array of TEdge;

operator <(e1, e2: TEdge)res: boolean;
begin
    res := e1.weight < e2.weight;
end;

operator >(e1, e2: TEdge)res: Boolean;
begin
    res := e1.weight > e2.weight;
end;

procedure SortEdge(A: TEdgeArr; l, r: longint);
var
    i, j: longint;
    t, m: TEdge;
begin
    i := l; j := r; m := A[(i+j) >> 1];
    repeat
        while A[i]<m do inc(i);
        while A[j]>m do dec(j);
        if i<=j then
        begin
            t := A[i];
            A[i] := A[j];
            A[j] := t;
            inc(i); dec(j);
        end;
    until i>j;
    if i<r then SortEdge(A, i, r);
    if l<j then SortEdge(A, l, j);
end;

const
    INF: int64 = 1<<60 div 3;
var
    map: array [1..100, 1..100] of int64;
    n, i, j: longint;

{
    @param x: 起始搜索节点
    算法思想：用一个数组维护从各个未加入顶点到
    树的最短边长度，操作n次，每次将距离最短的
    边加入到树中，并更新与之相邻的点的距离值。
}

function prim(x: longint): int64;
{
    lowest: 储存各个节点到树的最短距离
    visited: 标记是否已加入树中
}
var
    lowest: array [1..100] of int64;
    visited: array [1..100] of boolean;
    min: int64;
    i, j, minindex: longint;
begin
    fillchar(visited, sizeof(visited), 0);
    visited[x] := true;

    //先将初始节点加入树中，更新lowest
    for i := 1 to n do
        lowest[i] := map[i, x];

    prim := 0;
    for i := 2 to n do
    begin
        min := INF;

        //找出树到外部节点最短的一条边
        //并将该边加入树中
        for j := 1 to n do
            if (not visited[j]) and (min > lowest[j]) then
            begin
                min := lowest[j];
                minindex := j;
            end;
        visited[minindex] := true;
        prim := prim + min;

        //对新加入的那个节点，
        //更新与其相邻的未加入树的节点的lowest值
        for j := 1 to n do
        begin
            if visited[j] then continue;
            if map[j, minindex] < lowest[j] then
                lowest[j] := map[j, minindex];
        end;
    end;
end;

{
    算法思想：
    1\. 先将边按照长度排序。
    2\. 遍历所有的边，若该边的两个顶点都在树中则跳过；
    否则将其加入树中。
}

function Kruscal: int64;
var
    Edges: TEdgeArr;
    //并查集，储存自己的父亲，若自己为根结点则为自己
    //这是一种常用的写法：否则如果存成0的话，想把两棵
    //树并在一起需要多一步判断。
    UnionSet: array [0..100] of longint;
    i: longint;

    procedure InitEdges; //将邻接矩阵转化为边数组。
    var
        i, j: longint;
        E: TEdge;
    begin
        for i := 1 to n do
            for j := 1 to i-1 do
            begin
                E.start := i;
                E.terminal := j;
                E.weight := map[i, j];
                SetLength(Edges, Length(Edges)+1);
                Edges[High(Edges)] := E;
            end;
        SortEdge(Edges, Low(Edges), High(Edges));
    end;

    //寻找自己的根节点，并把自己直接连到根结点上。
    function Find(x: longint): longint;
    var
        root: longint;
    begin
        root := x;
        while root <> UnionSet[root] do
            root := UnionSet[root];
        UnionSet[x] := root;
        exit(root);
    end;

    //尝试将边的两个顶点并在一个并查集中，如果两个
    //顶点都在同一个集合中则返回False，否则执行合
    //并操作。
    function Union(x, y: longint): boolean;
    var
        px, py: longint;
    begin
        px := Find(x);
        py := Find(y);
        if px = py then
            exit(False);
        UnionSet[px] := py;
        exit(True);
    end;

begin
    Kruscal := 0;
    fillchar(UnionSet, sizeof(UnionSet), 0);
    InitEdges;
    for i := 1 to n do
        UnionSet[i] := i;
    for i := Low(Edges) to High(Edges) do
        if Union(Edges[i].start, Edges[i].terminal) then
        begin
            Kruscal := Kruscal + Edges[i].weight;
        end;
end;

begin
    assign(input, 'main.in'); reset(input);
    assign(output, 'main.out'); rewrite(output);

    readln(n);
    for i := 1 to n do
        for j := 1 to n do
            read(map[i, j]);
    writeln(Kruscal);

    close(input); close(output);
end.

NOIP2013 Day1 火柴排队：快速求逆序对

2014-10-26 | Tech

题目

涵涵有两盒火柴，每盒装有 n 根火柴，每根火柴都有一个高度。现在将每盒中的火柴各自排成一列，同一列火柴的高度互不相同，两列火柴之间的距离定义为： $$\sum_{i=1}^{n}{(a_i-b_i)^2}$$
其中 ai 表示第一列火柴中第 i 个火柴的高度，bi 表示第二列火柴中第 i 个火柴的高度。
每列火柴中相邻两根火柴的位置都可以交换，请你通过交换使得两列火柴之间的距离最小。请问得到这个最小的距离，最少需要交换多少次？如果这个数字太大，请输出这个最小交换次数对 99,999,997 取模的结果。

分析

这真是一道好题——断断续续想了几天才完全 AC。

事实上，由排序不等式可知：

$$当 a_i, b_i 从小到大排序时，距离最小$$

这是一个重要的信息。因此，我们只需把 $a_i,b_i$ 进行排序，并把对应项“捆绑”成一项，再按 $a_i$ 原有的顺序进行复原，此时，可以得到由 $b_i$ 原先的下标组成的一个序列。也就是说，我们要求 $1,2,\ldots,n$ 至少经过多少步才能变为该序列。这可以用逆序对来解决。

只可惜，传统的逆序对算法时间复杂度为 $O(n^2)$，这里 $n$ 可达 $200000$，一定会超时 ¹。因此我们需寻求更好的算法。

用归并排序求逆序对

在归并排序的过程中，有一个步骤称为合并。在这个步骤中，需要轮流判断左右区间的第一个数的大小关系。注意到：左右区间已经有序，从而若左区间的第一个数大于右区间的第一个数，则左区间之后的所有数都大于右区间的第一个数，从而我们可以在合并时做一些修改：

procedure nx(l, r: longint);
var
    mid, i, j, k: longint;
begin
    if l = r then
    begin
        tmp[l] := a[l];
        exit;
    end;
    mid := (l + r) shr 1;
    nx(l, mid);
    nx(mid+1, r);
    i := l;
    j := mid+1;
    k := l;
    while k <= r do
    begin
        if (j>r) or (i<=mid) and (a[i]<=a[j]) then //注意这里为等号
        begin
            tmp[k] := a[i];
            inc(i);
        end
        else
        begin
            cnt := cnt + mid - i + 1; //加上逆序数
            tmp[k] := a[j];
            inc(j);
        end;
        inc(k);
    end;
    for i := l to r do
        a[i] := tmp[i];
end;

这个算法复杂度为$O(n\log n)$，是一种比较理想的算法，实现起来也简单。但他有个缺点：会打乱原数组顺序。

原题代码

//AC
const
    MODN = 99999997;
type
    rec = record value, index: longint; end;
    TArr = array [1..100000] of rec;
var
    n: longint;
    a, b, c, tmp: TArr;
    ok: Boolean;
    l, r, i, j: longint;
    cnt: int64;

procedure sort(var arr: TArr; l, r: longint);
var
    i, j: longint;
    m, t: rec;
begin
    i := l;
    j := r;
    m := arr[(i+j) shr 1];
    repeat
        while arr[i].value < m.value do inc(i);
        while arr[j].value > m.value do dec(j);
        if i <= j then
        begin
            t := arr[i];
            arr[i] := arr[j];
            arr[j] := t;
            inc(i);
            dec(j);
        end;
    until i >j;
    if i < r then sort(arr, i, r);
    if l < j then sort(arr, l, j);
end;

procedure nx(l, r: longint);
var
    mid, i, j, k: longint;
begin
    if l = r then
    begin
        tmp[l] := c[l];
        exit;
    end;
    mid := (l + r) shr 1;
    nx(l, mid);
    nx(mid+1, r);
    i := l;
    j := mid+1;
    k := l;
    while k <= r do
    begin
        if (j>r) or (i<=mid) and (c[i].index<=c[j].index) then
        begin
            tmp[k] := c[i];
            inc(i);
        end
        else
        begin
            cnt := cnt + mid - i + 1;
            cnt := cnt mod MODN;
            tmp[k] := c[j];
            inc(j);
        end;
        inc(k);
    end;
    for i := l to r do
        c[i] := tmp[i];
end;

begin
    assign(input, 'main.in'); reset(input);
    assign(output, 'main.out'); rewrite(output);

    readln(n);
    for i := 1 to n do
    begin
        read(a[i].value);
        a[i].index := i;
    end;
    for i := 1 to n do
    begin
        read(b[i].value);
        b[i].index := i;
    end;
    sort(a, 1, n);
    sort(b, 1, n);

    for i := 1 to n do
        c[a[i].index] := b[i];

    cnt := 0;
    nx(1, n);
    writeln(cnt);

    close(input); close(output);
end.

事实上，只过了 70% 的点

NOIP2011 Day2 计算系数：快速求组合数

2014-10-25 | Tech

题目大意

输入 $a, b, k, n, m$，计算 $a^n\times b^m\times C_k^n$ 模 $10007$ 的余数。

分析

对于幂数的计算并不难，关键在于对组合数$C_n^k$的计算。

通常来说，组合数的计算一般是这样的：$$C_n^k=\frac{n}{k}\times\frac{n-1}{k-1}\times\ldots\times\frac{n-k+1}{1}$$ 这对于单精度的计算来说是十分快捷的，但如果要对结果取模的话就不起作用了——取模运算对于除法不成立。因此只能另辟蹊径了。

注意到加减乘法对于取模都是成立的，从而想到：能否将组合数转化成加法？我们自然而然想到了组合恒等式：$$C_n^k=C_{n-1}^{k}+C_{n-1}^{k-1}$$ 思路到此完成。

Code

const
    modn = 10007;
var
    a, b, k, m, n: longint;
    map: array[0..1000,0..1000] of int64; //缓存
//快速幂
function power(a, x: longint): int64;
var
    t: longint;
begin
    if x = 1 then
        exit(a);
    if x = 0 then
        exit(1);
    t := power(a, x shr 1);
    power := t * t mod modn;
    if odd(x) then
        power := power * a mod modn;
end;
//快速组合数
function C(n, k: longint): int64;
begin
    if map[n, k] > 0 then
        exit(map[n, k]);
    if (n <= k) or (k = 0) then
        C := 1
    else if k = 1 then
        C := n
    else
        C := (C(n-1, k)+C(n-1, k-1)) mod modn;
    map[n, k] := C;
end;

var
    t: longint;
    ans: int64;

begin
    assign(input, 'main.in'); reset(input);
    assign(output, 'main.out'); rewrite(output);

    readln(a, b, k, n, m);
    a := a mod modn;
    b := b mod modn;
    ans := power(a, n);
    ans := ans * power(b, m) mod modn;
    //C(k,n)与C(k,m)是等效的，计算较小者即可
    if n > m then n := m;
    ans := ans * C(k, n) mod modn;
    writeln(ans);

    close(input); close(output);
end.

UVa1647 Computer Transformation

2014-10-24 | Tech

链接：Link 耗时：0.679s

分析

本质上，这是一道求数列通项的题目。我们列出前几个字符串： $$01,$$ $$1001,$$ $$01101001,$$ $$1001011001101001,$$ $$\ldots$$

如果用$S_i$表示第 i 个字符串中“00”的个数，则有： $$S_1=0,\ S_2=1,\ S_3=1,\ S_4=3,\ S_5=5,\ S_6=11,\ldots$$

经过观察可以发现有如下规律： $$S_n=2\times S_{n-1}+{(-1)}^n$$

求通项就简单了，换个元即可： $$S_n=\frac{1}{3}[{(-1)}^n+2^{n-1}]$$

程序采用高精度实现。

Code

const
    JINDU = 100000;
var
    n: Integer;
//在数字前补0
procedure PrintANumber(x: longint);
var
    t: longint;
begin
    if x = 0 then
        write('00000')
    else
    begin
        t := JINDU;
        while t > x * 10 do
        begin
            write(0);
            t := t div 10;
        end;
        write(x);
    end;
end;

var
    ans: array [1..300] of longint;
    len, i: integer;
//计算2^(n-1)
procedure calc2;
var
    i, x, t, mul: longint;
begin
    len := 1;
    ans[1] := 1;
    t := n-1;
    while t > 0 do
    begin
        if t < 6 then
            mul := 1 << t
        else
            mul := 64;
        x := 0;
        for i := 1 to len do
        begin
            ans[i] := ans[i] * mul + x;
            x := ans[i] div JINDU;
            ans[i] := ans[i] mod JINDU;
        end;
        if x > 0 then
        begin
            inc(len);
            ans[len] := x;
        end;
        dec(t, 6);
    end;
end;
//除以3
procedure div3;
var
    i, x, t: longint;
begin
    i := len;
    x := 0;
    while i > 0 do
    begin
        t := (x * JINDU + ans[i]);
        ans[i] := t div 3;
        x := t mod 3;
        dec(i);
    end;
    while ans[len] = 0 do dec(len);
end;

begin
    assign(input, 'main.in'); reset(input);
    assign(output, 'main.out'); rewrite(output);

    while not eof do
    begin
        readln(n);
        if n=1 then   //特殊情况处理
        begin
            writeln(0);
            continue;
        end;
        fillchar(ans, sizeof(ans), 0);
        calc2;
        if odd(n) then
            dec(ans[1])
        else
            inc(ans[1]);
        div3;
        write(ans[len]);
        for i := len-1 downto 1 do
            PrintANumber(ans[i]);
        writeln;
    end;

    close(input); close(output);
end.

PREVNEXT

Code

问题描述

分析

Code

介绍

Code

引子

目录

题目

分析

用归并排序求逆序对

原题代码

题目大意

分析

Code

分析

Code