树状数组

2014-11-01 | Tech

介绍

所谓树状数组，就是将线性的数组预处理成树状的结构以降低时间复杂度。先来看一幅经典的图：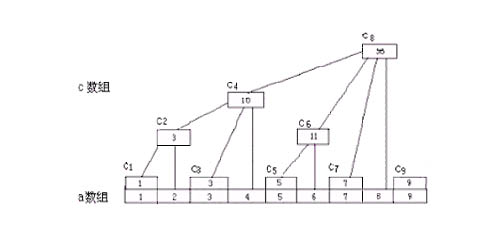

其中的 a 数组为原生数组，c 数组为辅助数组，计算方式为：

$$c_1=a_1——{(1)}_{10}={(1)}_2$$ $$c_2=a_2+c_1——{(2)}_{10}={(10)}_2$$ $$\ldots$$

不难发现，$c_k$存储的实际上是从 $k$ 开始向前数 $k$ 的二进制表示中右边第一个 $1$ 所代表的数字个元素的和。这样写的好处便是可以利用位运算轻松计算 sum。上代码。

Code

var
    n, i: longint;
    a, c: array [1..10000] of longint;

//计算x最右边的1所代表的数字。
//如：lowbit(0b1100)=0b100
function lowbit(x: longint): longint;
begin
    lowbit := x and (-x);
end;

//给a[index]加上x
procedure add(index, x: longint);
begin
    inc(a[index], x);
    while index<=n do
    begin
        inc(c[index], x);
        inc(index, lowbit(index));
    end;
end;

//求a[1~index]的和
function sum(index: longint): longint;
begin
    sum := 0;
    while index>0 do
    begin
        inc(sum, c[index]);
        dec(index, lowbit(index));
    end;
end;

var
    s: longint;
    op: longint;
    x,y: longint;

begin
    assign(input, 'main.in'); reset(input);
    assign(output, 'main.out'); rewrite(output);

    readln(n);
    for i := 1 to n do
    begin
        read(a[i]);
        add(i, a[i]);
    end;

    while not eof do
    begin
        read(op);
        if op = 1 then //添加操作
        begin
           read(x, y);
           Add(x, y);
        end
        else           //求和操作
        begin
            read(s);
            writeln(sum(s));
        end;
    end;

    close(input); close(output);
end.

作者：hsfzxjy
链接：
许可：CC BY-NC-ND 4.0.
著作权归作者所有。本文不允许被用作商业用途，非商业转载请注明出处。

NOIP Binary Indexed Tree

OOPS!

A comment box should be right here...But it was gone due to network issues :-(If you want to leave comments, make sure you have access to disqus.com.